Autores

B. Soares Neto, G. (IFB - INSTITUTO FEDERAL DE BRASÍLIA) ; M. S. Faria, K. (UFG - UNIVERSIDADE FEDERAL DE GOIÁS)

Resumo

O presente trabalho traz, de forma detalhada, o processo metodológico para obtenção de dados gemorfométricos de segunda ordem como curvatura vertical e curvatura horizontal. A compreensão dos algoritmos usados na modelagem das curvaturas possibilitaram determinar um método para obtenção das formas de relevo. Em ambiente SIG foi possível estabelecer álgebras de mapas entre os tipos de curvaturas que possibilitou a modelagem das formas de relevo do Distrito Federal. O resultado obtido permitiu a classificação das formas do relevo em nove classes. Os resultados obtidos também podem ser inseridos como variáveis em modelos de diagnósticos de risco a erosão e perda de solos, de movimento de massas, aptidão agrícola, entre outros.

Palavras chaves

Geomorfometria; Sistema de Informação Geográfica; Formas do Relevo

Introdução

Para Florenzano (2008), morfometria é a caracterização do relevo por meio de variáveis quantitativas, também denominadas índices morfométricos. Podemos, assim, entender que o estudo da morfografia é ponto de partida para o entendimento e classificação das feições geomorfológicas. Esta autora afirma, ainda, que a morfometria refere-se aos aspectos quantitativos do relevo, como as variáveis relacionadas às medidas de altura, comprimento, largura, superfície, volume, altura absoluta e relativa (declividade), curvatura, orientação, densidade e frequência de suas formas. A grande variação de métodos e atributos geomorfométricos apresenta a necessidade de um sistema incluindo diferentes técnicas e métodos de classificação das formas de terreno em um esquema que seja capaz de gerar os índices de uma superfície contínua (Schimidt e Dikau, 1999). Os dados geomorfométricos são de fundamental importância, pois permitem a modelagem de processos que possibilitará prognósticos ambientais e geotécnicos. Por exemplo, o gradiente de orientação é diretamente aplicado em funções relacionadas à geometria da superfície, ao balanço de radiação, no uso para agricultura, ou pode ser utilizado para estimativa da energia de transporte de material. Os atributos combinados descrevem e caracterizam a variabilidade espacial de processos específicos que ocorrem na paisagem, tais como a distribuição da umidade do solo e o potencial à erosão laminar e linear. Os índices combinados podem ser utilizados na modelagem de processos complexos, como o hidrológicos, geomorfológicos e biológicos. Pode-se, por exemplo, prever a distribuição espacial de diferentes espécies de plantas a partir do uso de índices de umidade e radiação solar, pois em muitos casos não é possível executar medidas diretas destes processos ambientais por limitações físicas, temporais ou econômicas. Já dados como curvatura vertical e horizontal são fundamentais, pois como expõe Valeriano (2008), há forte relação destes com o tipo de substrato e com processos de formação do relevo. Os estudos de compartimentação da topografia apontam a curvatura vertical como uma variável de alto poder de identificação de unidades homogêneas para mapeamentos diversos. Com relação a processos atuais, esta variável está relacionada aos processos de migração e acúmulo de matéria através da superfície (sobretudo água), proporcionados pela gravidade. Por este mecanismo, há atuação direta no equilíbrio entre os processos de pedogênese/morfogênese, além de influenciar a distribuição local do regime hídrico e, conseqüentemente, o regime térmico. Seja por sua atuação presente ou pretérita, a distribuição da curvatura vertical apresenta forte relação com mapas pedológicos e geológicos. Já a curvatura horizontal está relacionada à intensidade dos processos de migração e acúmulo de água, minerais e matéria orgânica no solo através da superfície, proporcionados pela gravidade. Analogamente à curvatura vertical, desempenha papel importante sobre o balanço hídrico e o equilíbrio entre os processos de pedogênese e morfogênese. Como medida de concentração do escoamento superficial, é uma variável importante também para a compreensão de problemas urbanos ligados ao posicionamento de estruturas de drenagem e mapeamento das possíveis áreas de alagamento. Neste contexto se insere o presente trabalho, cujo objetivo é determinar os processos metodológicos que possibilitam o controle na modelagem das formas de relevo do Distrito Federal, permitindo um maior entendimento das métricas que controlam a elaboração desses dados.

Material e métodos

2.1 – Topogrid (MDE) A geração do MDE foi realizada a partir da integração de dados geográficos feitos com o auxílio da plataforma ArcGis através do Topogrid (Topo to Raster) que é um método de interpolação especificamente projetado para a criação de modelos digitais de elevação hidrologicamente consistentes (MDE). Sua criação é baseada na metodologia de Michael Hutchinson (1988, 1989). 2.2 – Curvaturas (Formas das Vertentes) Analogamente à curvatura vertical, a curvatura horizontal pode ser expressa tanto em ângulo por distância como em raio de curvatura. Em ambiente SIG, a curvatura horizontal é baseada na comparação entre as orientações de vertente comparando-se nas células vizinhas ao uma célula de referência. Quando a orientação de vertentes da vizinhança for homogênea, resultarão valores baixos, caracterizando superfícies de forma planar. Tendo como referência Moore (1991), as curvaturas da área foram obtidas a partir de uma base matricial de altitude em que se calculou célula por célula e, para cada célula, foi determinado um polinômio de quarto, cuja formula é: Z = Ax²y² + Bx²y + Cxy² + Dx² + Ey² + Fxy + Gx + Hy + I Baseando-se em um arquivo matricial composto por células 3 x 3, os coeficientes de 'a' a 'i' são calculados a partir das relações altimétricas de vizinhança (Figura 01). Para a análise da curvatura vertical verifica-se a variação dos valores na direção X e na curvatura horizontal na direção Y, havendo uma análise linha a linha e coluna a coluna do arquivo matricial. As relações entre os coeficientes e os nove valores de elevação de cada célula numerada, determinam um modelo da superfície, como mostrado o diagrama seguinte (Figura 02): Por representar uma derivada de 2ª ordem da altimetria, após a obtenção do resultado de cada célula para obtenção do resultado das curvaturas devem-se relacionar pixels vizinhos a partir da seguinte expressão: Curvature = -2(D + E) * 100 Os dados obtidos no processamento geraram valores positivos e negativos, sendo que aqueles foram atribuídos às formas convexas e estes, às formas côncavas. Na prática, seria rara a ocorrência de valores nulos, que indicariam terrenos planos, com isso foi necessário considerar um intervalo que pudesse ser atribuído a superfícies planas. Segundo Valeriano (2008) ensaios comparativos com descrições geomorfológicas levaram ao estabelecimento da faixa entre -0,010º/m a 0,010º/m como valores de curvatura típicos de vertentes tidas como retilíneas. Assim, valores inferiores a este intervalo foram considerados como terrenos côncavos e valores superiores foram considerados como terrenos convexos. Da mesma forma que para curvaturas verticais, faz-se necessário o estabelecimento de uma faixa de valores admitidos como nulos para determinar a classificação das vertentes planares. Baseado nos testes feitos por Valeriano (2008) admitiu-se o intervalo de -0,038º a 0,051º/m para determinar superfícies planares, ocorrendo valores inferior a esse intervalo considerou o terreno como sendo convergente e superior ao intervalo como sendo divergente. As formas do terreno são obtidas a partir da combinação entre as curvaturas horizontais e verticais (Figura 03 A). Para Valeriano (2008), diante do interesse específico do estudo e das condições locais de terreno,substrato e processos vigentes, as classes de forma de terreno podem ser reagrupadas em função de sua similaridade frente a esses aspectos. Para determinar as formas do relevo foi feita uma análise de sobreposição usando as formas do relevo horizontal e vertical. Determinaram-se valores para cada tipo de curvatura e a soma desses valores representam uma determinada forma, conforme indicado na (Figura 03 B). Associou-se a cada dado raster, tanto de curvatura horizontal e vertical, valores atribuídos para as classes de curvatura, assim as células foram representadas a cada valor atribuídos. A soma dos dados raster permitiu a identificação dos tipos de forma.

Resultado e discussão

3 – RESULTADOS E DISCUSSÕES As vertentes, que para a geomorfologia são unidades básicas do relevo e fundamentais para explicar o desenvolvimento das paisagens, são descritas por Veloso (2002) como um elemento da superfície terrestre inclinado em relação ao plano horizontal. Vertente em seu sentido amplo significa superfície inclinada, independentemente de apresentar qualquer conotação genética ou local. Em uma definição mais restrita, é definida em geomorfologia como uma forma tridimensional que foi modelada pelos processos de denudação, atuantes no presente ou no passado, e que representa a conexão dinâmica entre o interflúvio e o vale (Christofoletti, 1980). Guerra (1993) define vertentes como planos de declives que divergem a partir das cristas enquadrando o vale. Nas zonas montanhosas, elas podem ser abruptas e formarem gargantas, estando mais próximas do leito dos rios. Quando as vertentes são relacionadas às planícies fluviais, estas são de difícil delimitação, pois são mais afastadas do leito. Essa é uma feição geomorfológica que pode apresentar formas muito variadas, porém é possível classificá-las de acordo com a sua curvatura que pode ser analisada no plano (curvatura horizontal) ou em perfil (curvatura vertical). Florenzano (2008) aponta a curvatura vertical das vertentes como uma das variáveis de alto poder de identificação de unidades homogêneas do relevo. A curvatura vertical refere-se à forma convexo/côncavo do terreno, quando analisado em perfil, podendo ser expressa em uma medida de ângulo, por meio de uma distância horizontal (graus por metro). Em ambiente SIG, seu cálculo é baseado na comparação entre diferenças altimétricas ao ponto da célula (pixel). As curvaturas se caracterizam por apresentar em valores positivos e negativos, dependendo da condição local, se côncava ou convexa. Já a curvatura horizontal é apontada por Florenzano (2008) como sendo o caráter divergente/convergente dos fluxos de matéria sobre o terreno e a sua percepção é feita através das direções de declive adjacente (denominada linhas de fluxo). As áreas em que essas linhas são paralelas têm curvatura horizontal nula e a superfície é caracterizada como planar. Áreas com linha de fluxo indicando convergência ou divergência têm curvaturas não nulas e de sinais opostos. Analogamente à curvatura vertical, a curvatura horizontal pode ser expressa tanto em ângulo por distância como em raio de curvatura. Em ambiente SIG, a curvatura horizontal é baseada na comparação entre as orientações de vertente comparando-se nas células vizinhas ao uma célula de referência. Quando a orientação de vertentes da vizinhança for homogênea, resultarão valores baixos, caracterizando superfícies de forma planar. A álgebra das curvaturas verticais e horizontais permitiram a obtenção das formas de relevo, possibilitando a sua classificação em nove formas distintas (Figura 04 D). A sua análise integrada as características do meio físico local (Geologia, Hidrografia, Clima, etc) indicam perspectivas sopre o processo pedogênese/morfogênese além influenciar a distribuição local do regime hídrico. As formas também se inserem como variáveis em modelos de diagnósticos de risco a erosão e perda de solos, de movimento de massas, aptidão agrícola, entre outros.

Representação de dado raster com identificação por célula.


Bloco diagrama de representando a extração dos dados de curvatura.


A Valores determinados para cada tipo de curvatura para representação do tipo de formas. B Tipos de curvatura .Fonte: adaptado de Dikau (1990)


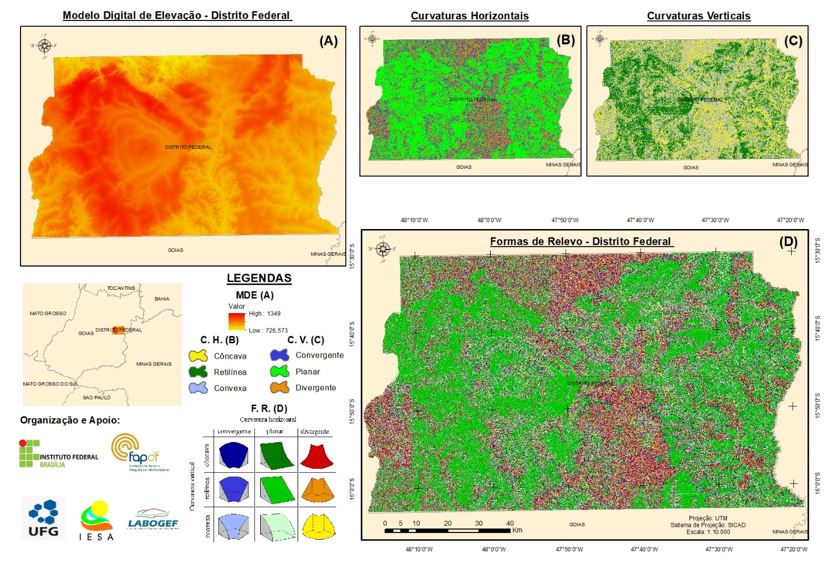
A Modelo Digital de Elevação. B Curv Horizontal. C Curv Vertical. D Formas de Relevo obtido pela álgebra entre a curvatura horizontal e Vertical.

Considerações Finais

O entendimento e o controle do processo permitiu representar de forma digital a medição das variáveis geomorfométricas, possibilitando a modelagem de dados do meio físico em ambiente SIG. Pois para Florenzano (2008), a inserção dessas variáveis em estudos multidisciplinares poderá promover o desenvolvimento de novos modelos e importantes avanços na aplicação daqueles existentes e tal avanço permite o uso de métodos para-métricos de análise de paisagem, para fornecer uma base mais objetiva e padronizada para a identificação de sistemas terrestres. Cabe ressaltar que, além do conhecimento do processo de geração das morfometrias e dos seus algoritmos, o acesso a dados topologicamente consistentes foi fundamental para obtenção de resultados que permitiram a modelagem terrestre mais próximo à realidade. Entender que as feições geográficas são representadas em forma de vetores em meio digital e que esta estrutura vetorial deve respeitar os relacionamentos espaciais dos fenômenos geográficos possibilita uma maior consistência no modelo da superfície terrestre. E por fim, pode-se concluir que o controle nos processos metodológicos para determinação de dados morfométricos contribuirá para diversas áreas do conhecimento, mas uma das áreas que fará mais uso é a geomorfologia, pois a representação geomorfológica faz uso das métricas do terreno para representar e caracterizar as superfícies do relevo.

Agradecimentos

Referências

CHRISTOFOLETTI, A. Geomorfologia. São Paulo, Editora Edgard Blücher, 1980.
DIKAU, R. Derivatives from detailed geoscientific maps using computer methods. Zeitschrift für Geomorphologie, v.80, p. 45-55, 1990.
FLORENZANO, T. G (org.). Geomorfologia: conceitos e tecnologias atuais. São Paulo: Oficina de Textos, 2008.
GUERRA, A.T. & GUERRA, A.J.T. Novo Dicionário Geológico-Geomorfológico. Rio de Janeiro, Bertrand Brasil, 2ª edição. 2001. 648p.
HUTCHINSON, M.F. A new procedure for gridding elevation and stream line data with automatic removal of spurious pits. Journal of Hydrology 106: 211-232, 1989.
HUTCHINSON, M.F. Calculation of hydrologically sound digital elevation models. Paper presented at Third International Symposium on Spatial Data Handling at Sydney, Australia, 1988.
MOORE, I.D., R. B. Grayson, and A. R. Landson. Digital Terrain Modelling: A Review of hydrological, Geomorphological, and Biological Applications. Hydrological Processes 5: 3–30, 1991.
SCHIMIDT, J. & DIKAU, R.(1999). Extracting geomorphometric attributes and objects from digital elevation models – Semantics, methods, future needs. GIS for Earth Surface Systems – Analysis and Modeling of the Natural Environment. Dikau, R. & Saurer, H. Borntraeger, (eds.). Stuttgart, 197 p.
VALERIANO, M. M. TOPODATA: Guia para utilização de dados geomorfológicos locai. São Jose dos Campos: INPE, 2008.
VELOSO, A. J. G. Importancia do Estudo das Vertentes. GEOgraphia. v.8, n.8, 2002
WAHBA, G. Spline models for Observational data. Paper presented at CBMS-NSF Regional Conference Series in Applied Mathematics. Philadelphia: Soc. Ind. Appl. Maths, 1990.