Autores
Silveira, R.M.P. (UFPR) ; Silveira, C.T. (UFPR)
Resumo
O presente trabalho tem como objetivo aplicar uma classificação geomorfométrica para mapear formas de relevo e formas de vertente num recorte localizado na Serra do Mar, estado do Paraná, Brasil, a partir de um Modelo Digital do Terreno (MDT) derivado de base planialtimétrica na escala 1:25.000 e sete atributos topográficos (declividade, plano de curvatura, perfil de curvatura, relevo sombreado, acumulação de fluxo, índice topográfico de umidade e índice de posição topográfica). As regras de classificação automatizada foram definidas por critérios estatísticos e critérios determinísticos. O mapa de formas de relevo resultou na identificação de cinco formas de relevo principais (planície, rampas coluvionares, calhas de drenagem, vertentes e cristas) fragmentadas em outras oito adicionais. Para o mapa de formas de vertente foram obtidas 27 classes. Em campo constatou-se o potencial de aplicação das classificações para levantamentos geomorfológicos preliminares.
Palavras chaves
Modelo Digital do Terreno; Geomorfometria; Mapeamento Geomorfológico
Introdução
A modelagem geomorfológica, amparada pela disponibilidade cada vez maior de Modelos Digitais do Terreno (MDT) e capacidade otimizada de processamento em ambiente de Sistemas de Informações Geográficas (SIG), configura um cenário favorável para a crescente aplicação da análise digital do relevo como suporte na construção de diversos mapeamentos temáticos. A geomorfometria, definida como a ciência da análise quantitativa da superfície terrestre (PIKE, 2000), tem como enfoque a extração de medidas descritivas (parâmetros) e feições da superfície terrestre (objetos) (MARK e SMITH, 2004; WILSON, 2012). Evans (1972) define a primeira, que trata a superfície de modo contínuo, como geomorfometria geral, e a segunda, que contempla a discretização da superfície, como geomorfometria específica. O presente trabalho contempla as duas abordagens. Conforme Minar e Evans (2008), a análise digital do relevo tem como grande desafio suprir a falta de precisão e objetividade dos mapeamentos geomorfológicos tradicionais. Entretanto, destaca-se que as classificações automatizadas de formas de relevo quase sempre representam uma tentativa de replicar algum sistema previamente concebido de classificação e mapeamento manual de formas de relevo. Muitos desses sistemas manuais consideram modelos semânticos que tentam contemplar conceitos considerados importantes pelo pesquisador utilizando a formulação de critérios subjetivos para a diferenciação de classes (MACMILLAN e SHARY, 2009). Nesse contexto, a descrição numérica da geometria da superfície, associada à relação entre topografia, processo e forma, possibilita a criação de um conjunto consistente de regras para a delimitação de unidades do relevo (ROMSTAD, 2001). Referente à complexidade associada à caracterização determinística de formas de relevo e outras unidades/entidades geomorfológicas, Bishop et al. (2012) sinalizam cinco dificuldades principais: a) estabelecimento de esquemas taxonômicos compreensivos; b) mapeamento geomorfológico em diferentes escalas; c) caracterização de limites indeterminados e áreas de transição; d) estabelecimento de critérios aplicados universalmente; e) obtenção de resultados reproduzíveis. Diversos autores apontam as vantagens da classificação geomorfológica digital apoiada por técnicas geomorfométricas (DIKAU et al., 1991; WOOD, 1996; MACMILLAN et al., 2000; WILSON e GALLANT, 2000; ROMSTAD, 2001; VALERIANO, 2004; DRAGUT e BLASCHKE, 2006; IWAHASHI e PIKE, 2007; PIKE et al., 2009; SAADAT et al., 2008; WILSON, 2012; SILVEIRA et al., 2014), sobretudo em função da redução da subjetividade na classificação manual, facilidade na comparação dos resultados derivados de diferentes conjuntos de dados e da redução do tempo de delineação das unidades ou feições individualizadas. Nesse cenário, o presente trabalho tem como objetivo aplicar uma classificação geomorfométrica, a partir de MDT e atributos topográficos, num recorte localizado na porção central da Serra do Mar Paranaense. A classificação que resultou nos mapas de formas de relevo e formas de vertente teve como referência a hierarquia taxonômica de Ross (1992), adotada pelo mapeamento geomorfológico do estado do Paraná (SANTOS et al., 2006; OKA-FIORI; 2006). O recorte definido como área de estudo, inserido no contexto da Serra do Mar, está localizado na porção leste do estado do Paraná e compreende quatro cartas topográficas na escala 1:25.000. Abrange parcialmente quatro municípios paranaenses: Morretes, Guaratuba, Paranaguá e, numa pequena porção a sudeste, Matinhos. Totaliza área de 686,2 km². Destaca-se que a área de estudo contempla uma das regiões mais atingidas pelos movimentos de massa ocorridos em março de 2011. Devido à intensidade do evento, a região ainda encontra-se instável e suscetível ao desprendimento e remobilização de material. Os trabalhos de campo se concentraram na bacia hidrográfica do rio Jacareí e sub-bacia do rio Tingidor, cujo destaque é representado em todos os produtos cartográficos.
Material e métodos
A elaboração dos mapas de formas de relevo e formas de vertente foi dividida em duas etapas: a) modelagem e caracterização geomorfométrica; b) definição das regras de classificação geomorfológica. Os trabalhos de campo balizaram o mapeamento tanto nas etapas prévias, com a definição das principais feições identificadas na área de estudo, quanto na conferência posterior, in loco, das classificações obtidas. O Modelo Digital do Terreno foi gerado com base no método de interpolação denominado Topogrid, baseado na proposta de Hutchinson (1988), a partir de dados planialtimétricos vetoriais (curvas de nível, pontos cotados e hidrografia). As cartas topográficas utilizadas foram: 2858-1 NE, 2858-1 SE, 2858-2 NO, 2858-2 SO, na escala 1:25.000 (DSG, 2002). A etapa de definição da resolução horizontal (célula ou pixel) do MDT foi pautada em contribuições de Hengl (2006), considerando as características topográficas locais e complexidade do terreno. Nessa proposta, a resolução horizontal do MDT pode ser estimada numa relação entre as curvas de nível e área, sendo: p = A / 2 . ∑L, onde p é o tamanho do pixel, A é a área total e ∑L é o somatório do comprimento de todas as curvas de nível do recorte avaliado. Com base no resultado de 16,3 metros obtido na área de estudo, o tamanho de pixel adotado para o MDT foi definido em 15x15 metros, totalizando uma grade de 1671x1875 pixels para toda a área de estudo. A partir do MDT foram calculados sete atributos topográficos: declividade, relevo sombreado (conforme variáveis direcionais de Horn (1981)), plano e perfil de curvatura (ZEVENBERGEN e THORNE, 1987), acumulação de fluxo (utilizando o algoritmo D-Infinito de Tarboton (1997)), Índice Topográfico de Umidade (BEVEN e KIRKBY, 1979) e Índice de Posição Topográfica (WEISS, 2001) – além da altimetria, que é o próprio MDT. Com exceção do IPT, todos os demais atributos foram calculados a partir de janelas móveis de vizinhança 3x3 células. O Índice de Posição Topográfica (IPT), proposto por Weiss (2001), é derivado de um algoritmo que mensura a diferença entre a elevação de um ponto central (Z0) e a média da elevação (Z) ao seu redor com um raio predeterminado (R). Wilson e Gallant (2000, p. 74), apresentando a mesma equação, definem o cálculo como Diferença da Elevação Média: IPT = Z0 - Z. Após a fase inicial de definição das classes a serem mapeadas, em campo, as regras de classificação automatizada foram definidas considerando duas abordagens: a) discretização dos atributos topográficos por critérios estatísticos (média e desvio padrão) para variáveis que apresentam valores relativos a uma área específica, como acumulação de fluxo, e valores que variam em função do fator de escala, como o IPT; b) discretização por critérios determinísticos para variáveis cujos valores podem ser aplicados em áreas distintas, como declividade e hipsometria. Para o mapa de unidades de relevo foram definidas 13 classes detalhadas derivadas da combinação de atributos topográficos particionados pelo processo de álgebra de mapas. Foram utilizadas as seguintes variáveis: hipsometria, declividade, acumulação de fluxo, ITU e IPT. As regras de classificação são representadas pela figura 1. O mapa de formas de vertente foi resultado da combinação entre plano e perfil de curvatura (parâmetros destacados na figura 2), representando nove formas elementares (DIKAU, 1989; MACMILLAN e SHARY, 2009). Adicionalmente acrescentou-se a declividade para indicar a inclinação destes segmentos de vertente, cujas combinações totalizam 27 classes.
Resultado e discussão
O mapa de formas de relevo (figura 1) resultou na identificação de cinco
formas de relevo principais (planície, rampas coluvionares, calhas de
drenagem, vertentes e cristas) fragmentadas em outras oito adicionais,
subdivididas em classes com distintas características geomorfométricas. A
classificação contemplou as principais segmentações morfológicas da área de
estudo, com poucos ruídos na classificação.
As classes de formas de relevo identificadas se mostraram adequadas tanto em
termos de diversidade das feições características presentes na área de
estudo quanto de representatividade adequada à escala geomorfológica
pretendida, indicando a fragmentação das subunidades morfoesculturais.
Na bacia hidrográfica do rio Jacareí, local onde se concentraram as etapas
de conferência em campo. Em todos os casos, seja na planície ou nos topos da
serra, as feições mapeadas pela classificação foram facilmente observadas in
loco, principalmente as cristas, as vertentes (terço médio e terço superior
da Serra do Mar, com forte controle estrutural) e a planície. As calhas de
drenagem de vertente também foram representadas de modo fidedigno, com
méritos para o MDT Topogrid utilizado, ainda que muitos segmentos tenham
apresentado descontinuidades, sobretudo na planície, cujo fluxo acumulado
dessas áreas é menor que nas vertentes devido à baixa variação de
declividade.
Em campo constatou-se o potencial de aplicação da classificação para
levantamentos geomorfológicos preliminares, condizente com as principais
rupturas observadas na paisagem, embora as limitações desse modelo se
atenham sobretudo na definição dos limites e áreas de transição: onde
termina uma crista e onde se inicia uma rampa coluvionar, por exemplo.
Essa constatação reforça uma questão central da análise digital do relevo
aplicada ao mapeamento de formas de relevo: a relação interdependente entre
a geometria e a topologia, entre o quantitativo e o qualitativo, entre o
mensurável e o subjetivo. Referente à imprecisão dos limites obtidos pela
classificação, destaca-se essa é uma problemática que emerge da percepção
conceitual qualitativa e inevitavelmente acaba sendo transposta para as
etapas de atribuição de parâmetros que visam a representação de
descontinuidades topográficas. Nesse sentido, denota-se que o mapeamento
automatizado reduz a subjetividade em aspectos operacionais, visando a
reprodutibilidade e padronização metodológica, embora o intermédio com as
definições qualitativas (conceituais e semânticas) da geomorfologia ainda
mantenha parte da subjetividade do mapeamento.
Exemplo disso, no trabalho, foi a separação entre cristas e topos de serras
das cristas e topos de morros, uma vez que em muitos casos as propriedades
morfométricas destas duas unidades são semelhantes e a própria qualificação
descritiva é imprecisa. Comumente a literatura aponta que morros são
elevações que variam de 100 até 300 metros de altitude, entretanto muitas
elevações secundárias com essas características são encontradas nas porções
intermediárias da Serra do Mar. Daí a necessidade de acrescentar a
delimitação do 3º táxon do mapeamento geomorfológico do estado do Paraná
como regra de classificação, pois em casos específicos, ligados a aspectos
genéticos, apenas a morfometria pode não ser capaz de distinguir formas com
origens variadas.
Ademais, independentemente da distinção genética, os morros isolados
localizados sobretudo à norte da área de estudo foram todos mapeados
adequadamente em contraste ao declive constante da planície. Para essa
segmentação de grandes unidades geomorfológicas o IPT foi o atributo
topográfico que apresentou os melhores resultados.
Para o mapa de formas de vertente foram obtidas 27 classes (figura 2).
Devido ao nível de detalhamento, as formas de vertente se mostraram mais
sensíveis à qualidade e à escala do modelo. Assim, a análise dos resultados
obtidos considera tanto a equidistância das curvas de nível (10 metros) da
base cartográfica utilizada como referência para a interpolação do MDT
quanto a janela local de vizinhança (3x3) para o cálculo do plano e perfil
de curvatura e da declividade.
O mapa deste nível identificou segmentos predominantes de vertente
condizentes à escala 1:25.000 que localmente podem apresentar variações não
mapeadas pela limitação dos dados de entrada.
Devido à sensibilidade da modelagem observada para esta classificação, a
alteração de parâmetros, por menores que sejam, desde as etapas iniciais de
elaboração do MDT até as regras de classificação, afeta diretamente o
produto final. Se, por um lado, o rigor metodológico deve ser priorizado com
ainda mais ênfase, de outro as dificuldades relacionadas à conferência em
campo e atribuições qualitativas aumentam proporcionalmente às
possibilidades de critérios adotados na classificação ao nível pretendido de
semidetalhe, chegando aos segmentos de vertente.
Pelo fato desta classificação considerar segmentos predominantes de
vertente, em campo algumas feições são mais facilmente identificadas que
outras. Oportunamente ressalta-se um aspecto interessante das
classificações: embora a base cartográfica utilizada para interpolação do
MDT seja de 2002 e os eventos de movimentos de massa tenham ocorrido em
2011, com drásticas mudanças na paisagem local, os modelos indicaram as
formas características de relevo que influem na dinâmica dos processos
atuantes.
A classe de maior representatividade na área de estudo foi o segmento
retilíneo-planar, com declividade inferior a 6%. Dentre as limitações desta
classificação, além da adequação paramétrica, destacam-se a miscelânea de
informações e dificuldades de representação em escala compatível e a
subjetividade da validação e/ou simples conferência in loco. Quanto às
potencialidades, destaca-se a possibilidade de integração de variáveis
adicionais voltadas para aplicações específicas, principalmente a aspectos
morfodinâmicos.
Destaca-se, também, a dificuldade em estabelecer relações hierárquicas das
feições mapeadas entre os níveis taxonômicos. No Mapeamento Geomorfológico
do estado do Paraná, os três níveis taxonômicos mapeados representam uma
hierarquia: o "Cinturão Orogênico do Atlântico" (1º táxon, unidade
morfoestrutural), por exemplo, é constituído pelas unidades morfoesculturais
"Serra do Mar" e "Primeiro Planalto" (2º táxon) e estes, na área de estudo,
são fragmentados entre outras 10 subunidades morfoesculturais (3º táxon).
Entretanto, nos mapeamentos propostos para esse recorte da Serra do Mar, por
exemplo, não seria possível agrupar cicatrizes de deslizamento em uma única
classe de forma de vertente. As formas de vertente, por sua vez, também não
configuram com exatidão os limites das classes do mapa de formas de relevo.
E estes, por fim, não têm agrupamento específico definido para caracterizar
o 3º táxon do mapeamento utilizado como referência.
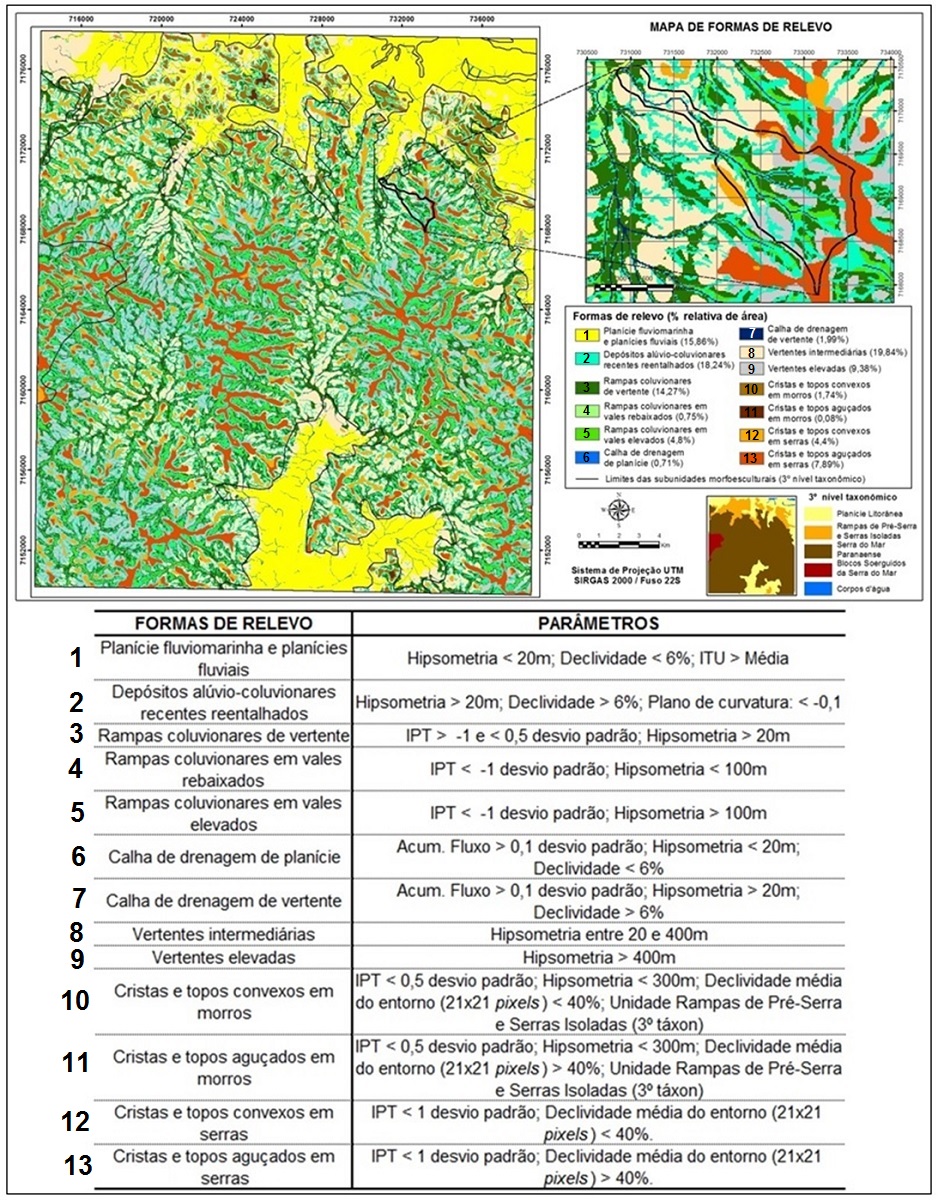
Mapa de formas de relevo (com destaque para a sub- bacia hidrográfica do rio Tingidor) e parâmetros de classificação.
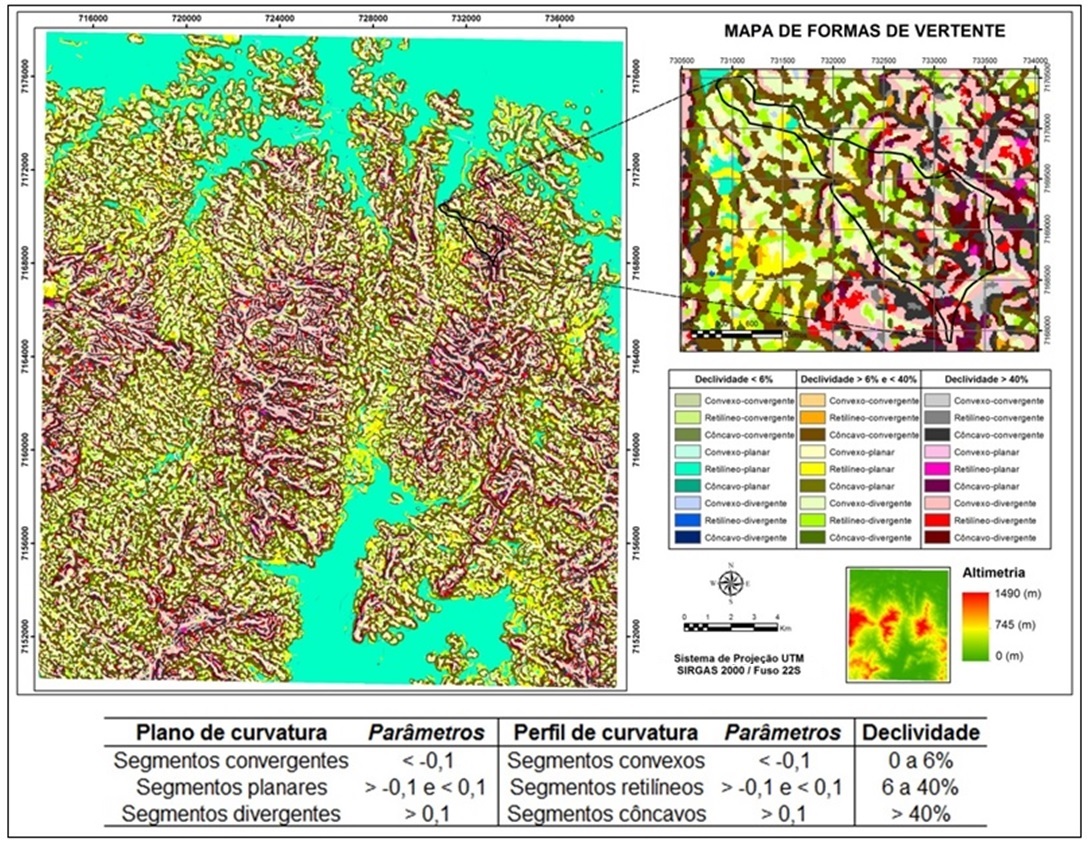
Mapa de formas de vertente (com destaque para a sub-bacia hidrográfica do rio Tingidor) e parâmetros de classificação.
Considerações Finais
A aplicação das propostas de classificações geomorfométricas automatizadas a partir de MDT e atributos topográficos derivados evidenciou a possibilidade de realizar levantamentos geomorfológicos preliminares com baixo custo operacional e representatividade na paisagem desde que considerada a importância do rigor metodológico para a eficácia da classificação resultante. Os atributos topográficos que melhor representaram a segmentação geomorfológica da área de estudo foram a declividade, o plano e perfil de curvatura e o índice de posição topográfica. As curvaturas tiveram maior variação conforme a mudança de resolução horizontal do MDT, portanto sua aplicação está condicionada ao fator de escala. Nessa perspectiva, reforça-se que o objetivo da classificação deve condizer com alguns tópicos fundamentais que determinam a aplicabilidade do produto final: a escala da base de dados, o tamanho de célula do MDE, o cálculo dos atributos topográficos, o tamanho da janela móvel para cálculos de vizinhança e as regras de classificação parametrizada. Embora a proposta tenha demonstrado potencial para identificar feições geomorfológicas que auxiliam a construção de mapas geomorfológicos, sua aplicação é dependente de parâmetros mutuamente compatíveis e da inclusão de outros atributos topográficos e/ou regras de classificação.
Agradecimentos
À CAPES, pela concessão de bolsa de estudo, e ao Laboratório de Pesquisas Aplicadas em Geomorfologia e Geotecnologias (LAGEO/UFPR), pelo suporte durante o desenvolvimento do trabalho.
Referências
BEVEN, K. J.; KIRKBY, M. J., A physically based, variable contributing area model of basin hydrology. Hydrological Sciences Bulletin 24 (1), 43–69, 1979.
BISHOP, M. P.; JAMES, L. A.; SHRODER, J. F.; WALSH, S. J. Geospatial technologies and digital geomorphological mapping: Concepts, issues and research. Geomorphology 137, p. 5–26, 2012.
DIKAU, R. The application of a digital relief model to landform analysis. In: RAPER, J. F. (Ed.), Three Dimensional Applications in Geographical Information Systems. Taylor & Francis, London, pp. 51–77, 1989.
DIKAU, R.; BRABB, E. E.; MARK, R. M. Landform Classification of New Mexico by Computer. Open File report 91-634. U.S. Geological Survey, 1991.
DRAGUT, L; BLASCHKE, T. Automated classification of landform elements using object-based image analysis. Geomorphology, 81, 330–344, 2006.
DSG - Diretoria do Serviço Geográfico do Exército Brasileiro. Cartas Topográficas: folhas 2858-1 NE; 2858-1 SE; 2858-2 NO; e 2858-2 SO. DSG, 2002.
EVANS, I. S. General geomorphometry, derivatives of altitude, and descriptive statistics. In: CHORLEY, R. J. (Ed.). Spatial analysis in geomorphology. London: Harper & Row, Publishers, 1972.
HENGL, T. Finding the right pixel size. Computers & Geosciences 32, 1283–1298, 2006.
HORN, B. K. P. Hill shading and the reflectance map. Proceedings of the IEEE, n. 69, v.01, p. 14-47, 1981.
HUTCHINSON, M. F. Calculation of hydrologically sound digital elevation models. Paper presented at Third International Symposium on Spatial Data Handling at Sydney, Australia, 1988.
IWAHASHI, J.; PIKE, R. J. Automated classifications of topography from DEMs by an unsupervised nested-means algorithm and a three-part geometric signature. Geomorphology 86(3-4): 409-440, 2007.
MACMILLAN, R. A.; PETTAPIECE, W. W.; NOLAN, S. C.; GODDARD, T. W. A generic procedure for automatically segmenting landforms into landform elements using DEMs, heuristic rules and fuzzy logic. Fuzzy Sets and Systems 113, 81–109, 2000.
MACMILLAN, R. A.; SHARY, P. A. Landform and landform elements in geomorphometry. In: HENGL, T.; REUTER, H. I. (eds.) Geomorphometry - Concepts, Software, Applications, Series Developments in Soil Science vol. 33, Amsterdam: Elsevier, pp. 227-254, 2009.
MACMILLAN, R. A.; SHARY, P. A. Landform and landform elements in geomorphometry. In: HENGL, T.; REUTER, H. I. (eds.) Geomorphometry - Concepts, Software, Applications, Series Developments in Soil Science vol. 33, Amsterdam: Elsevier, pp. 227-254, 2009.
MARK, D. M., SMITH, B. A science of topography: from qualitative ontology to digital representations. In: Bishop, M.P., Shroder, J.F. (Eds.), Geographic Information Science and Mountain Geomorphology. Springer–Praxis, Chichester, England, pp. 75–97, 2004.
MINÁR, J.; EVANS, I. S. Elementary forms for land surface segmentation: the theoretical basis of terrain analysis and geomorphological mapping. Geomorphology 95 (3–4), 236–259, 2008.
OKA-FIORI, C., SANTOS, L.J.C., CANALI, N.E., FIORI, A.P., SILVEIRA, C.T., SILVA, J.M.F., ROSS, J.L.S. Atlas Geomorfológico do Estado do Paraná: escala base 1:250.000, modelos reduzidos 1:500.000. Curitiba, MINEROPAR, 2006.
PIKE, R. J. Geomorphometry — diversity in quantitative surface analysis. Progress in Physical Geography 24 (1), 1–20, 2000.
PIKE, R. J.; EVANS, I., HENGL, T. Geomorphometry: A Brief Guide. In: HENGL, T.; REUTER, H. I. (eds.) Geomorphometry - Concepts, Software, Applications, Series Developments in Soil Science vol. 33, Amsterdam: Elsevier, pp. 3-30, 2009.
ROMSTAD, B. Improving relief classification with contextual merging. Proceedings of ScanGIS'2001 — The 8th Scandinavian Research Conference on Geographical Information Science. Ås, Norway, p. 3–13, 2001.
ROSS, J. S. Registro cartográfico dos fatos geomorfológicos e a questão da taxonomia do relevo. Rev. Geografia. São Paulo, IG-USP, 1992.
SAADAT, H.; BONNELL, R.; SHARIFI, F.; MEHUYS, G.; NAMDAR, M.; ALE-EBRAHIM, S. Landform classification from a digital elevation model and satellite imagery. Geomorphology 100, p. 453–464, 2008.
SANTOS, L.J.C.; OKA-FIORI, C.; CANALI, N.E.; FIORI, A.P.; SILVEIRA, C.T.; SILVA, J.M.F.; ROSS, J.L.S. Mapeamento geomorfológico do Estado do Paraná. Revista Brasileira de Geomorfologia. Ano 7, n°2, p. 3-12, 2006.
SILVEIRA, R. M. P.; SILVEIRA, C. T.; OKA-FIORI, C. Emprego de técnicas de inferência espacial para identificação de unidades de relevo apoiado em atributos topográficos e árvore de decisão. Revista Brasileira de Geomorfologia, v. 15, nº 1, 87-101, 2014.
TARBOTON, D. G. A New Method for the Determination of Flow Directions and Contributing Areas in Grid Digital Elevation Models. Water Resources Research, 33(2): 309-319, 1997.
VALERIANO, M.M. Modelo digital de elevação com dados SRTM disponíveis para a América do Sul. Instituto Nacional de Pesquisas Espaciais, p. 1-72, 2004.
WEISS, A. Topographic Position and Landforms Analysis. Poster presentation, ESRI User Conference, San Diego, CA, 2001.
WILSON, J. P. Digital terrain modelling. Geomorphology, 137, p.107–121, 2012.
WILSON, J. P.; GALLANT, J. C. (eds.). Terrain analysis: principles and applications. New York: John Wiley & Sons, p.1-27, 2000.
WOOD, J. The geomorphological characterisation of digital elevation models. PhD Thesis - University of Leicester. Disponível em: http://www.soi.city.ac.uk/~jwo/phd. Leicester, UK, 185p., 1996.
ZEVENBERGEN, L. W.; THORNE, C. R. Quantitative Analysis of Land Surface Topography. Earth Surface Processes and Landforms, v.12, p.47-56, 1987.
